Combining factor inputs AP Microeconomics

AP® Microeconomics:
3.4 Factor input combinations

Topics in the factor markets unit studied thus far in AP® Microeconomics have so far focussed on individual factors of production. However, firms employ different combinations of factor inputs (land, labor, capital and enterprise) and the profit maximizing firm must be able to determine the most cost-effective combination of inputs to employ for any given level of output. The cost minimization rule is based on the principles of marginal analysis and this is used to maximize a firm's profits when different combinations of factor inputs are employed.

Factor input combinations – Topics:

Input combinations
Substitutes and complements in production
Cost minimization
Profit maximization

Factor input combinations

Learning objectives

Explain that firms use different combinations of factors of production in producing their goods and services
Distinguish between substitutes and complements in factor markets
Calculate total costs associated with different combinations of factor inputs being employed, and determine the optimal combination
Use marginal analysis to explain the cost-minimization rule
Use the cost-minimization rule to calculate the most efficient use of factor inputs
Determine the output level that maximizes profits for firms using different factor input combination

Alternative Input Combinations

In most cases a firm can choose among a number of alternative combinations of factor inputs that will produce a given level of output. Firms will want to choose the most cost effective factor input combination to achieve a given level of output.

For example, on Annabel’s wheat farm where land is fixed in the long-run, the short-run factor input decision may involve consideration of different combinations of labor and capital. To produce the optimal quantity of wheat, she could choose to have a capital-intensive operation and invest in tractors and mechanized farm equipment and hire limited numbers of farm workers (labor). Alternatively, she may choose a combination of inputs that is more labor-intensive. Annabel would then choose factor input combinations where she would hire more farm workers to do most planting and harvesting by hand. The same quantity of output (tons of wheat) could be produced using different combinations of labor and capital. Annabel would need to determine the exact combination of factor inputs that would maximize her profits; i.e., the lowest cost factor input combination of labor and capital to produce her desired output.

To examine the optimal combination of factor inputs, we turn our attention to the relationship between the factor inputs that are used in production. We can classify factor inputs as being either substitutes or complements in the production of goods and services..

Substitutes and Complements in Factor Markets

The concepts of substitutes and complements do not just apply to consumption in product markets, they also apply to production in factor markets; i.e. a firm’s purchase of factor inputs. And just as the price of related goods affects consumers’ purchasing decisions, the price of other inputs can affect a firm’s decision about how much of an input it will use.

Capital and labor can be substitutes or complements. For example, as substitutes, Annabel could produce the same quantity of wheat if she substituted more tractors for less farm labor. Likewise, ATM machines (a capital good) can be substitutes for bank tellers (labor) in the production of financial services.

Capital and labor may also be complements in the production process. This occurs when adding an additional unit of either labor or capital increases the marginal product of the other factor of production.

An example would be the increase in labor productivity that occurs when Annabel purchases a tractor (a capital good), as farm workers become more productive when Annabel purchases the tractor, and each tractor requires labor to drive it. Office workers become more productive when they use faster computers running better software, and doctors have become more productive with the use of modern X-ray machines and other diagnostic equipment.

In each of these cases increases in the quantity and quality of capital available increases the marginal product of labor, which in turn, increases the demand for labor. Given the relationship between inputs, how does a firm determine which of the possible combinations to use?

Capital and LABOR PRODUCTIVITY

MULTIFACTOR PRODUCTIVITY

the Optimal Input Mix

Profit = total revenue - total costs. Minimizing total costs helps to maximize profits. If different alternative factor input combinations can be used to produce the optimal level of production output, the profit-maximizing firm should select the combination of inputs that have the lowest cost. A process known as cost minimization.

Cost Minimization

How can a firm determine the combination of factor inputs that maximizes its profits? We will use an example to consider this question.

Annabel owns and manages a chain of bakeries and she needs to decide the best combination of relatively expensive industrial ovens and bakers at a new bakery. The table below shows the different combinations of capital (industrial ovens) and labor (bakers) she can hire to bake the cakes that the bakery produces. If the bakery puts in 20 industrial ovens, she will need to hire one baker to use the ovens to produce cakes. That is five industrial ovens for each baker, which is a total of four cashiers.

However, the bakery has the option of running two shifts, so the bakery could produce the same number of cakes using ten bakers and ten industrial ovens. If the bakery can produce the same number of cakes using either of these factor input combinations of capital and labor, how does she decide which of these different combination of inputs she should use? The answer is to find that particular input combination which costs the bakery the least; i.e., the cost-minimizing input combination.

Assume that the cost to rent, operate, and maintain an industrial oven for a month is $1,000 and hiring a baker costs $1,600 a month. The cost of each factor input combination in the table above. The calculation of the cost of each combination of factor inputs is shown below.

All things being equal, Annabel's bakery would choose the lower cost combination, combination B, and employ ten bakers and put in ten industrial ovens.

Firms choosing between alternative combinations of inputs will evaluate the cost of each input combination and select that combination that minimizes their costs of production. One way to do this is to calculate the total cost of each alternative input combination, as shown here in this example. However, in reality the possible input combinations that the firm could use can be large. Thus, marginal analysis is a more practical method of finding the cost minimizing level of output – this is the cost-minimization rule.

Marginal cost of production

Diminishing marginal returns

The Cost-Minimization Rule

The additional output that is produced when an additional unit of an input (e.g., unit of labor) is employed is the marginal product (MP) of that input. Firms aim to achieve the greatest marginal product possible from each dollar they spend on the inputs to production. To achieve this, firms will adjust the ratio of employment inputs until the marginal product per dollar is equal for all factor inputs; and this is the cost-minimization rule.

If the firm's inputs are labor and capital, the cost-minimizing rule means that the marginal product of labor (MPL) per dollar spent on wages is equal to the marginal product of capital (MPK) per dollar spent to rent capital:

MPL/Wage = MPK/Rental rate

Cost minimization occurs when the marginal product per dollar is equal for all labor and capital inputs because if the cost of an additional input is lower, then it is less expensive to employ an additional unit of that factor input (e.g., labor) than it was to employ the additional unit of the other factor input (e.g., capital)

For example, consider the following situation where the marginal product of labor per dollar is greater than the marginal product of capital per dollar:

MPL/Wage > MPK/Rental rate

If, for example, the marginal product of capital is 100 units and the marginal product of labor is 20 units. If the rental rate for capital is $100 and the wage rate is $10, then the marginal product per dollar will be 100/$100 = 1 units of output per dollar for capital and 20/$10 = 2 units of output per dollar for labor; i.e., MPL/Wage > MPK/Rental rate

The firm would receive only 1 additional unit of output for each dollar it spends on capital, whereas it would receive 2 additional units of output for each dollar it spends on labor. The profit maximizing firm will minimize costs to produce a given level of output.

In this example, the firm gets greater additional output per dollar spent by employing labor, thus, it should rent less capital and employ more labor. Diminishing marginal returns means that as the firm employs additional units of labor, the marginal product of labor decreases and by employing fewer units of capital, the marginal product of capital increases. The profit maximizing firm continues to substitute labor for capital until the decreasing marginal product of labor per dollar equals the increasing marginal product of capital per dollar, and MPL/Wage = MPK/Rental rate. Therefore, by using marginal analysis, the firm adjusts its employment of capital and labor until the marginal product per dollar spent on each input is equal.

Let us now consider an example where the marginal product of labor per dollar is less than the marginal product of capital per dollar:

MPL/Wage < MPK/Rental rate

In this example, the marginal product of capital for the last unit of capital hired is 100 units and the marginal product of labor for the last unit of labor hired is 20 units. If the is rental rate for capital is $25 and the wage rate is $10, then the marginal product per dollar will be 20/$10 = 2 units of output per dollar for labor and 100/$25 = 4 units of output per dollar for capital. The firm receives only 2 additional units of output for each dollar spent on labor whereas it gains 4 additional units of output for every dollar that it spends on capital.

In this example, the firm obtains greater additional output for each dollar it spends by employing capital, and therefore it should employ less labor and more capital to maximize its profits.

Again, due to the law of diminishing marginal returns, as additional units of capital are employed then the marginal product of capital decreases, and by substituting capital for labor, less labor units are employed, causing the marginal product of labor to increase.

The profit maximizing firm continues to substitute capital for labor until the decreasing marginal product of capital per dollar equals the increasing marginal product of labor per dollar, and MPL/Wage = MPK/Rental rate. Therefore, by using marginal analysis, the firm adjusts its employment of capital and labor until the marginal product per dollar spent on each input is equal.

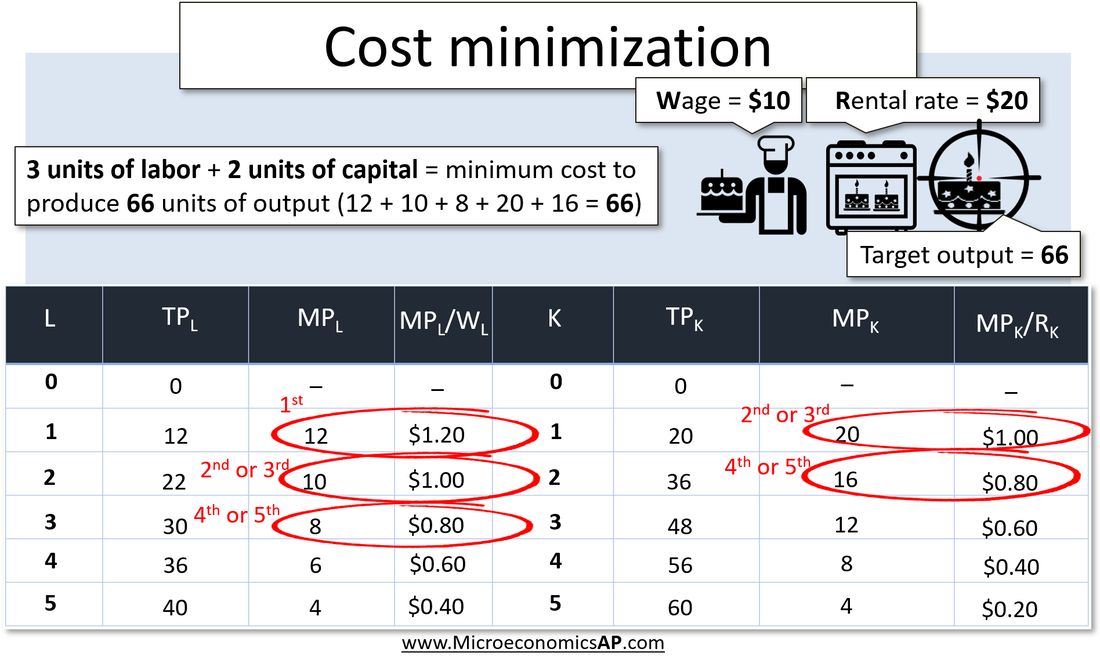
Loss minimizing combinations

When determining the cost minimizing combination of resources, we must first divide the marginal product of the factor input by the factor price. In the above example, the price of labor (L) is $10 per unit and the price of capital (K) is $20 per unit. For simplicity, we will assume that labor and capital are substitutes in production, meaning that there is not a certain amount of labor required to operate the capital.

If we were assigned to produce an output level of 66 units, what combination of labor and capital should we employ?

The first unit of labor gives 1.2 units of output per dollar compared to only 1 unit of output per dollar for capital, so the firm should use the labor first. Since this provides only 12 units of output, the firm needs to employ more resources. The second unit of labor and the first unit of capital have the same marginal product per dollar, so the firm would be indifferent to which it employs first and since it needs both, the firm will employ each.

Still needing more factor inputs to reach its output level of 66 units, the firm compares the third unit of labor and the second unit of capital. Both have the same marginal product per dollar and again, the firm needs both to reach its given output level. Thus, it will employ three units of labor and two units of capital to produce 66 units of output.

Profit maximizing combinations

Finding the cost minimization combination of resources to produce a given output level is a necessary but not a sufficient condition for profit maximization. The firm must also determine the output level that maximizes profits.

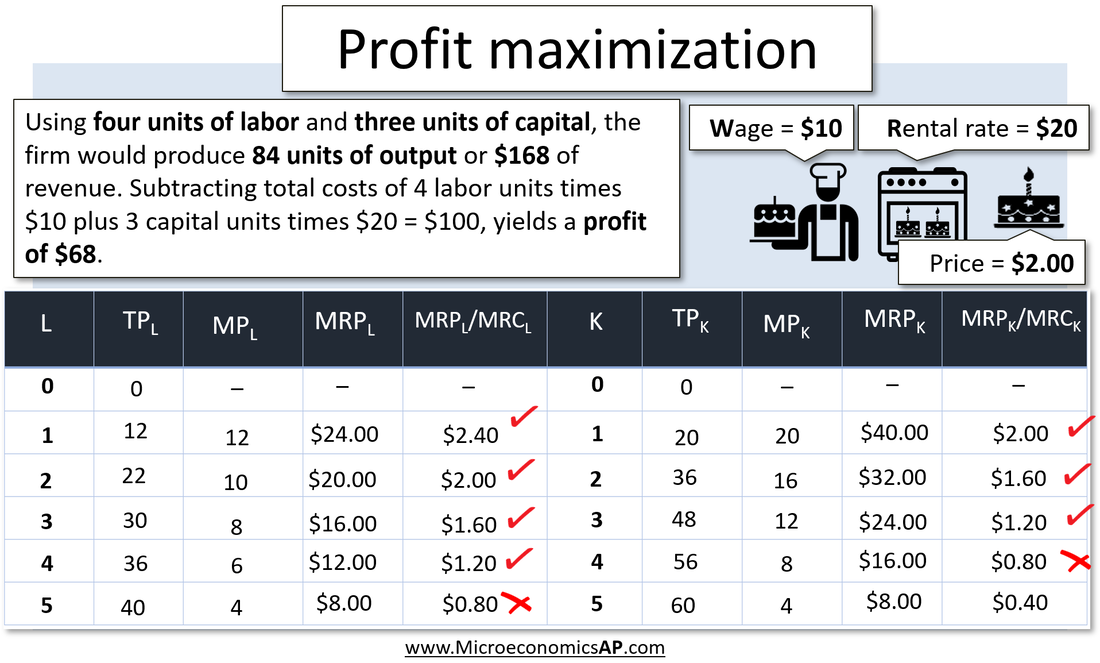
As discussed earlier, a firm must compare the marginal revenue product to the marginal resource cost of using the resource. By dividing the MRP by MRC, we can compare the additional revenue generated per dollar cost of the resource.

For example, if the MRP/MRC is $2, then the firm is generating two dollars of revenue for every dollar of cost of the resource.

For example, assume that the price of output is $2 per unit and the price of labor is $10 and the price of capital is $20. To determine the profit maximizing input level, the firm would first calculate the marginal revenue product for each input then divide it by the resource price or marginal resource cost.

It then determines which inputs, if employed, would add more additional revenue than cost. In looking at labor, it would employ four units. If it employed the fifth unit, the firm would only generate 80 cents of revenue per dollar cost.

In looking at capital, the firm would employ three units of capital. If labor and capital were the only costs, the firm could then determine the resulting profit. Using four units of labor and three units of capital, it would produce 84 units of output and $168 of revenue.

Subtracting total costs of 4 labor units times $10 plus 3 capital units times $20 = $100, yields a profit of $68.

AP® MICROECONOMICS – POWERPOINT SUMMARY NOTES:
3.4 Factor input combinations

CHECK YOUR UNDERSTANDING BY COMPLETING THE ACTIVITIES BELOW

You have below, a range of practice activities, flash cards, exam practice questions and an online interactive self test to ensure you have complete mastery of the AP® Microeconomics requirements for the Factor Input Combinations topic.